《教學構思~五下怎樣列式？》

《教學構思~五下怎樣列式？》

「算術思考」→…gap…→「代數思考」

一個不斷地遊走於模糊地帶的議題

在中小學的課程中，「一元一次方程式」這課題

橫跨了三年，從小五到國一

為何需要三年呢？三個禮拜不行嗎？三個月不行嗎？
是定量或變量?  是未知數或變數?  能釐清嗎?

小五的訓練重點是什麼呢？

五節課的規劃如下：

先進行「簡記活動」，然後從中歸納「列式規則」，接著利用「思考演變圖」讓孩子有個全觀，然後用「表徵變換九宮格」讓孩子遊走於格式間，最後「引入線段圖」並從中歸納等價式。

Section one 【簡記活動】

註：簡記活動的發展是源自於甯平獻教授所提的「算式填充題」，以及攻讀學位時的啟發。

一、初體驗
1.老師口語佈題，刻意讓題目又臭又長，逼迫孩子要做「註記」
2.請孩子協助，把剛剛的口語佈題記錄在黑板上(此時，孩子故意讓老師寫很多，一字不漏)

3.老師這麼辛苦寫這麼多，你們剛剛也寫這麼多嗎？如果沒有，那你們寫了什麼？然後，要求孩子「原汁重現剛剛的解題草稿」(上台)

4.接著老師一一檢視，並給予鼓勵

5.指出「註記或解題草稿」的兩大標準：「懶(不須太費時間)」又「不會太懶(具備溝通功能)」

二、練習

1.口語佈題，題目又臭又長，逼迫孩子要做註記
2.請孩子協助，把問題記錄在黑板上，But「文字描述也盡可能精簡」，精簡後的結果就是一般的數學問題

3.要求孩子原汁重現剛剛的解題記錄(上台)
4.老師依照兩大標準一一檢視，並《給予不同的建議與計分》，其功能在於收斂孩子的想法

註：剛開始熱身，留點空間讓孩子發揮，並多累績一點經驗吧!

Section two 【列式原則】

先帶孩子走一下上一節課的內容

然後提問
Q1:三種方法相同之處？

孩子的分享

這題目非常抽象，要想辦法讓孩子逐漸聚焦，才有辦法。引導之法就難以記錄了～但也花了一節課
歸納三個原則

Section three 【心智地圖】

今日繪畫主題【思考的演變】，分為五個階段A-精簡後的文字題B-記號或解題草稿C-算式填充題D-解題E-答案，其中B和D讓孩子盡情揮灑，具多樣性，C和E則是幫忙收斂，做個結尾

有五個目的

1.讓孩子有全觀
2.老師出題，直接從B-記錄開始，示範不同的記號模式
3.繼續收C-列示(算式填充題)
4.在D-解法中，讓孩子盡情揮灑，待日後再收
5.老師可以視班級情況，提高問題難度

Section four 【表徵變換九宮格】

天氣太熱了…昏昏欲睡
來做點練習
一、畫上九宮格，準備出三題數學問題
二、各題的出題方式不同，第一題是文字題，第二題是畫圖表示，第三題是列式表示
三、接著，帶領孩子把剩餘的六個空格完成

四、接著，當作回家功課，要孩子模仿出題
Next把收回來的作業當考卷，分成六回，每回寫一題，然後再交回給出題者批閱

Section five 【引入線段圖】

引入線段關係圖，並歸納等價關係式

一、部份全體關係
1.出算式填充題，請學生畫圖
2.檢討後，提出畫圖的一些限制，並介紹線段圖
3.學生練習線段圖

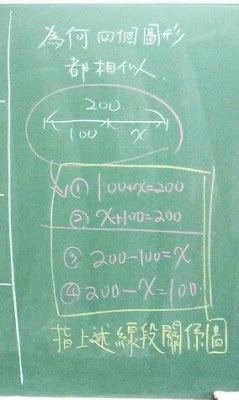
4.提出思考題，為何四個圖相似
5.從中，歸納等價關係式

二、巢狀關係
1.換乘除等價關係系列，一樣出算式填充題，請學生畫圖、畫線段圖，8小題
2.學生發表，老師檢討

3.提出思考題
4.歸納，在小學，目前先分兩類

然後可以試著提升一點點難度，帶著孩子「鋪謎→解謎」