教學實錄-六下-從「分類」解決「模式」問題
「分類」在數學上的重要不遑多論,要窮盡且互斥,
從物理性質中歸納……到等價關係,無不分類。
今天任務的重點是透過「分類」和「算式記錄」形成「模式(pattern)」,然後「推廣」。
「佈題」
師:看一下,一邊有5個圈圈的空心正方形,周圍有幾個圈圈?
生:16個
師:那4個圈圈的呢?
生:12個
師:那3個圈圈的呢?
生:8個
師:怎麼算?1.2.3 .4.5.6.7.8
師:那4個圈圈的呢?也用數的嗎?寫成算式怎麼寫?1+1+1…嗎?
師:有沒有其它寫法?
「生發表,老師記錄」圖不清楚sorry,如下:
a.
1+1+1+1+1+1+1+1+1+1+1+1=12(一個一個數)
b.
4+4+2+2=12(上下,再左右)
c. 3+3+3+3=12(包含一個角)
d. 4×4-2×2=12(先填再扣)
e. 4×4-4=12(先4邊再扣角)
「模式選擇」
師:如果排成每邊35個圈圈的空心隊形,共有幾人?
師:你們要一個一個數嗎?不會吧!想想看,怎麼算?
「模式競爭」
師:如果是五邊形的呢?怎麼算?用先填再扣嗎?不會吧!
引出「分類」一詞
師:我們來看看這些不同的算法,他的根源是什麼?
師:其實是分類,怎麼分類,就會導致後續所採取的作法。我們看一下
如果我們把「中間3個和1個角」當成一類,就會用左圖的方式計算
如果我們把圖形分成「內」和「外」,就會用右圖的方式計算
「推廣」
師:我們再來看看之前的例子
其實,這也是用分類的技巧
左圖:我們把上下分成一類,這類是有規則的:4×N;而左右是一類,這類永遠只有2。
右圖:我們把最左邊這一邊分成一類,這類永遠只有1;而接下來的「一橫一斜」分成一類,這類是有規則的:2×N。
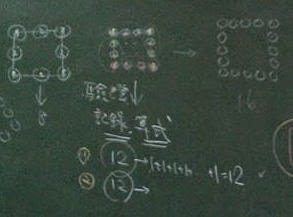






沒有留言:
張貼留言