教案設計-五上-因數和倍數-1
1/2
目標:源自於【數學教學構念-五上-因數和倍數】的規劃,本部分處理公因數的定性與定量問題。
Begin
引子
有一個年輕人買了一間小小的公寓,其中一片小小的牆面想要鋪磁磚,做點造型。這時候,這年輕人就打電話請賣磁磚的老闆送樣本過來,但這年輕人有一個特別的藝術欣賞嗜好,他希望老闆送過來的磁磚是「正方形」的。我們來看看接下來發生什麼事。
核心問題一~
以「公因數」解題的問題
師:這年輕人的牆面其實很小,就只有6cm × 8cm ,所以老闆心想,既然這年輕人喜歡正方形的磁磚,所以就只帶了一個樣本1cm × 1cm 給年輕人看;這年輕人看了看,覺得不是很滿意,希望老闆再換換磁磚。孩子們,你們猜看看,這老闆下次帶過來的磁磚是多大的磁磚?
生:2cm × 2cm 就可以啊!
師:還有嗎?
生:3cm × 3cm 也可以啊!
師:我們來畫看看可不可以,不可以,那還有嗎?
子活動一~
畫圖嘗試,或採計算的方式
師:這年輕人希望在另一個牆面也鋪設磁磚,這個牆面大了一點12cm × 18cm ,也是需要正方形磁磚,你們覺得老闆會帶多大的磁磚過來呢?1cm × 1cm 是可以的、2cm × 2cm 也是可以的,還有嗎?(發下學習單、小組討論)
子活動二~
透過「除除再乘」展現因數的概念
師:我們知道,磁磚小一點就需要很多塊,例如1cm × 1cm 的磁磚就需要12×18=216塊,但若磁磚大一點,就不用這麼多塊,但到底是幾塊呢?
師:孩子們在計算塊數時,似乎有兩種方法,請你們解釋一下兩種方法的想法。(設法讓先除除再乘的方法出頭,後續活動需要)
核心問題二~
檢視核心問題一的穩定性
師:這年輕人又需要磁磚了,這次這面牆更大了,是60cm × 24cm ,也是需要正方形磁磚,你們覺得老闆會帶多大的磁磚過來呢?每種磁磚需要的個數是多少呢?我們畫一個表格記錄一下。
師:如果是1cm × 1cm 需要60×24=1440個;那如果是2cm × 2cm 需要幾個?我們之前有兩種算法,今天請孩子們練習這個方法,60÷2=30、24÷2=12、30×12=360個,接下來的給大家試看看。
子活動三~
檢視「定量」的穩定性
師:(回家功課)有一天這年輕人變成大富翁了,他有一面牆240cm × 600cm ,你們覺得老闆會帶多大的磁磚過來呢?每種磁磚需要的個數是多少呢?請畫一個表格記錄一下。
核心問題三~
發展求公因數的算則
師:我們來看看昨天的問題,6cm × 8cm 的牆面。因為年輕人需要正方形的磁磚,所以老闆在店裡可以先把正方形的磁磚1×1、2×2、…8×8都拿出來,因為一邊是6cm ,所以可以刪掉一些磁磚,因為另一邊是8cm ,所以再刪掉一些磁磚。
師:那如果是60cm × 80cm 的牆面,我們可以怎麼做呢?(小組討論)
師:我們來看看要怎麼做?
師:直接從60的因數著手…
【反省】
1.因為孩子們早就有使用因數、倍數來解題的經驗,只是小四之前並不特別用因數、倍數來稱呼。而本次的教學則建立在上述的假設下,直接佈出公因數的問題,期望孩子先藉由畫圖嘗試,對問題的本質有「定性」的了解,再透過數字的加大,為了增加解題速度,發展出求因數、公因數的需求。
2.核心問題一是採示範的模式,引導孩子進行嘗試。子活動一時,雖然數字還不是很大,但若還採無方向的嘗試,將面臨更多繁瑣的嘗試或計算。子活動二是一個附加價值的學習,而且透過「除除再乘」的計算求磁磚個數,其實已經充分展現因數的概念。
3.核心問題二是核心問題一的練習,「收」的活動。
4.核心活動三是將孩子們選擇磁磚大小的過程「詳細記錄」,透過記錄,再逐步化繁為簡,最後形成算則。




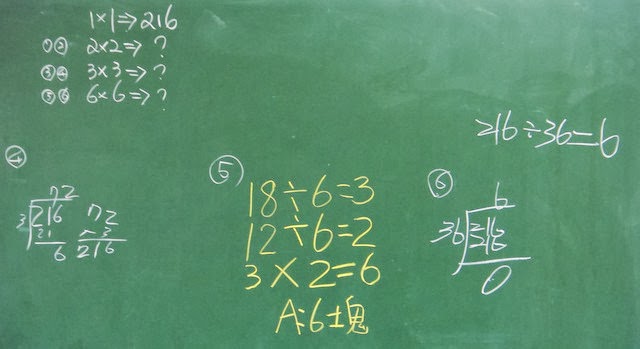




沒有留言:
張貼留言